Bomb Cyclones: What’s Behind all the Drama?

Storm Eunice, 18.02.2022 (Source: EUMETSAT)
If you want to attract attention to something, start by giving it a catchy name. In the sober world of geophysical fluid dynamics, most important phenomena are given worthy but boring names like the “North Atlantic Oscillation” or “Walker Circulation.” Occasionally, however, more interesting names appear, like the “Beast from the East”, “Thermohaline Catastrophe”, or “Bomb Cyclone”. These all manage to combine the exotic with a hint of violence.
A “bomb cyclone” is a mid-latitude storm that exhibits explosively fast development. The first official description of a particular kind of cyclone as a “Bomb” was in the title of an academic paper by Frederick Sanders and John Gyakum in 1980. For a cyclone to qualify as a “bomb”, its central surface pressure must drop by at least 24 mb in 24 hours. If you prefer the metric units, that is 24 hPa in 24 hours. In other words, the pressure drop must be large, and must happen very fast. That combination makes the occurrence of bomb cyclones relatively rare.
Bomb cyclones tend to occur mostly over the mid-latitude oceans during winter. The archetypal “bomb” (or “perfect storm”) occurs in the North Atlantic off the east coast of the U.S. when cold, dry air from the North American continent travelling to the east and south runs up against warmer, moist air from the sub-tropical Atlantic. That encounter sets up a steep temperature gradient, especially at the surface. While nature may abhor a vacuum, thermodynamics abhors a gradient and will try to reduce it.
Compared to average storms, the rapid fall in central pressure is the extreme element of a Storm Eunice type weather event. The pressure drop in a common-or-garden mid-latitude storm is more typically 10-15 mb in 24 hours, while normal day-to-day fluctuations in surface pressure around Ireland would be about 3-6 mb. At the other extreme, storm Barra (Fig. 1), which made a direct hit on Ireland in December 2021, was something of a megaton “bomb”: its central pressure fell from 1010 to 956mb (i.e., 54mb) in 24 hours. It is a testament to the quality of modern weather forecasting, and modern emergency preparedness, that the damage and destruction caused by Barra was much less extreme than the storm itself!
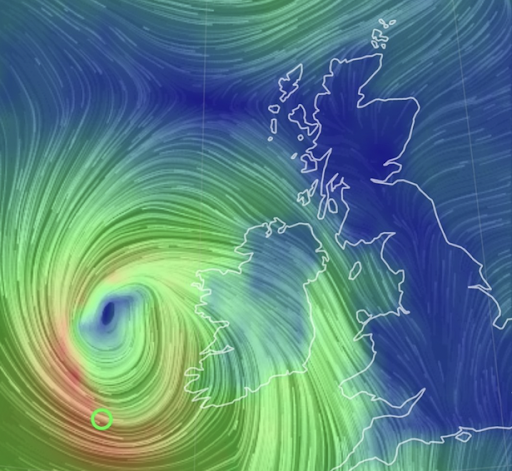
Figure 1. Storm Barra developing off the west coast of Ireland, 7 Dec. 2021
The central pressure of a cyclonic storm dropping by 24 mb in 24 hours (i.e., a “bomb” cyclogenesis), is not the same as the pressure at a fixed point dropping by the same amount in the same time. If an “old” pressure system with 1010mb at its edges and 980mb at its centre moves over Valentia, barometers in Valentia will register a 30mb drop in pressure even though the storm itself has not changed at all. Valentia will likely experience strong winds and rain from that storm, but technically, it's not a “bomb”.
For a fluid (like the atmosphere) on the surface of a rotating sphere (like the earth), the appearance of a steep surface temperature gradient requires the flow to initiate new unstable circulations in response, and it will do this on a typical cyclone scale (~ 1,000km). These cyclonic circulations carry warm air into the cold zone, and cold air into the warm zone where ultimately (after several days) they mix and so kill off the locally rotating circulations – along with the original temperature gradient. Of course, cold dry air is denser than warm moist air, so as they flow towards each other the warm air is pushed over the cold air, condensing out its moisture as it rises, leading to clouds and rain. Moreover, to satisfy all the balances required of a fluid on a rotating sphere like the earth, the original temperature gradient has an associated surface pressure gradient, which in turn requires winds to blow perpendicular to the gradient (i.e., along the pressure contours, or isobars), just turned down-gradient a bit due to surface friction. The whole thermodynamic effort of trying to smooth out the large-scale temperature gradient is a very twisted process (literally). It involves 3-dimensional structures in temperature, pressure, wind, and moisture fields all choreographed together in what we know as a mid-latitude cyclone.
Bomb cyclones have all the same attributes of a normal mid-latitude winter storm as described above. The only feature that distinguishes them, and makes them “bombs”, is their explosive growth. For meteorologists back in 1980 (including Sanders and Gyakum), trying to understand how such explosively fast growth could happen was a real problem. The mathematical concepts and tools that were used to explain the instabilities behind mid-latitude cyclones all produced growth rates that were much too slow to explain “bombs”. It took a series of papers through the 1980s by Brian Farrell of Harvard University, motivated by the 1907 work of William Orr of the Royal College of Science for Ireland, to provide a complete picture of how “bombs” could grow so fast.
In a nutshell, the original, inadequate, theories for cyclone development were based on so-called “normal modes” (i.e., eigenvector solutions of a set of linear equations); waves that had rigid structures that could grow in size but not change their shape over time. The insight of Farrell and Orr was that instabilities like bomb cyclones can grow out of initial small wavy structures that are more flexible and can grow at different rates in different places, changing their shape as they grow. Mathematically they can be found by applying a variational principle, which searches through all possible structures to find e.g., the fastest-growing one, or the one that grows the most over a fixed time; say, 24 hours.
The picture presented by Farrell is of an initial wave structure that is initially folded down like the bottle-separators in a case of wine, but leaning against the prevailing background wind shear (Fig. 2). As time moves on, the background wind “stands up” the wave, causing it to amplify (and develop lower surface pressure), and it can do this very fast. Of course, as time moves on further, the background wind blows the structure over in the opposite direction, weakening it again. However, that initial transient growth can generate storms that are large enough for nonlinear effects to dominate, and delay the eventual weakening.
The original idea (and solution) of transient growth of an initial wave like this “leaning against” the shear is due to Orr’s paper in 1907 in the Proceedings of the Royal Irish Academy.
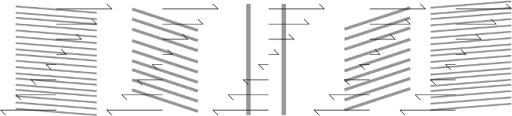
Figure 2. Schematic image of the Orr mechanism in action.
The thick grey lines represent the disturbance structure (shown in vertical cross-section), with the thin arrows showing background wind. The original structure is tightly compressed, but leans against the wind shear, which blows it over and amplifies it before blowing it over in the other direction, weakening it again. From Bedrossian et al. (2018)
It takes a lot of mental and intestinal fortitude to read all 70 pages of Orr’s paper now – and I confess I don’t have such fortitude. The papers by Farrell are more accessible. Even so, probably all that most of us need to know about how bomb cyclones manage to grow so deep so fast, is that the initial disturbances are so flexible, and so aligned and tilted against the shear that they can grow at different rates in different places as they allow themselves to be blown over by the background wind. Non-bomb cyclones can develop by this mechanism too, of course, only their initial configuration is just not so optimally aligned.
Meanwhile, the more rigid “normal modes” don’t allow themselves to be blown over like this. In a sense, they must devote some of their energy to keeping their shape and resisting the background shear instead of just literally going with the flow. While they grow more slowly, they also grow more steadily, and like the tortoise beating the hare, they can emerge once the initial explosive but transient growth phase of the bomb cyclone is over. Once any linear structure (whether modal or non-modal) reaches finite amplitude, nonlinear effects emerge and numerical simulations must replace analytic mathematics to reveal what goes on in more mature storms.
With modern mathematical and modelling techniques, along with satellite data and imagery, meteorologists can now provide remarkably accurate predictions two or three days ahead of bomb cyclone development, giving society time to prepare for the worst effects of storms like Barra and Eunice. While the detailed research of Orr and Farrell may seem arcane, it is work like theirs that gives us the most profound understanding of how bomb cyclones develop in the real world. If you can understand the dynamics controlling the behaviour of the differentially heated atmosphere on the rotating earth, you realise that these complex, intrinsically 3-dimensional storm structures are not merely accidental, but rather necessary features of our winter weather.
References
Bedrossian, J. Y. Deng and N. Masmoudi, 2018. The Orr Mechanism: Stability/Instability of the Couette Flow for the 2nd Euler Dynamic. Proc. Int. Cong. of Math., Rio de Janeiro, Vol. 3, p.2155-2184. https://eta.impa.br/dl/138.pdf
Farrell, B. F. (1982). The Initial Growth of Disturbances in a Baroclinic Flow, Journal of Atmospheric Sciences, 39(8), 1663-1686. Retrieved Feb 18, 2022, from https://journals.ametsoc.org/view/journals/atsc/39/8/1520-0469_1982_039_1663_tigodi_2_0_co_2.xml
Farrell, B. (1984). Modal and Non-Modal Baroclinic Waves, Journal of Atmospheric Sciences, 41(4), 668-673. Retrieved Feb 18, 2022, from https://journals.ametsoc.org/view/journals/atsc/41/4/1520-0469_1984_041_0668_manmbw_2_0_co_2.xml
Farrell, B. (1985). Transient Growth of Damped Baroclinic Waves, Journal of Atmospheric Sciences, 42(24), 2718-2727. Retrieved Feb 18, 2022, from https://journals.ametsoc.org/view/journals/atsc/42/24/1520-0469_1985_042_2718_tgodbw_2_0_co_2.xml
Farrell, B. (1987). Developing Disturbances in Shear, Journal of Atmospheric Sciences, 44(16), 2191-2199. Retrieved Feb 18, 2022, from https://journals.ametsoc.org/view/journals/atsc/44/16/1520-0469_1987_044_2191_ddis_2_0_co_2.xml
Farrell, B. F. (1989). Optimal Excitation of Baroclinic Waves, Journal of Atmospheric Sciences, 46(9), 1193-1206. Retrieved Feb 18, 2022, from https://journals.ametsoc.org/view/journals/atsc/46/9/1520-0469_1989_046_1193_oeobw_2_0_co_2.xml
O'Brien, E. (1992). Optimal Growth Rates in the Quasigeostrophic Initial Value Problem, Journal of Atmospheric Sciences, 49(17), 1557-1570. Retrieved Feb 18, 2022, from https://journals.ametsoc.org/view/journals/atsc/49/17/1520-0469_1992_049_1557_ogritq_2_0_co_2.xml
Orr, W.M., 1907: The Stability or Instability of the Steady Motions of a Perfect Liquid and of a Viscous Liquid. Part II: A Viscous Liquid. Proceedings of the Royal Irish Academy. Section A: Mathematical and Physical Sciences , 1907 - 1909, Vol. 27 (1907 - 1909), pp. 69-138. https://www.jstor.org/stable/20490591
Sanders, F., & Gyakum, J. R. (1980). Synoptic-Dynamic Climatology of the “Bomb”, Monthly Weather Review, 108(10), 1589-1606. Retrieved Feb 17, 2022, from https://journals.ametsoc.org/view/journals/mwre/108/10/1520-0493_1980_108_1589_sdcot_2_0_co_2.xml